RL Problem


The Settings

  • Agent’s Actions: Goal is to maximize expected cumulative reward
  • Env
  • Rewards

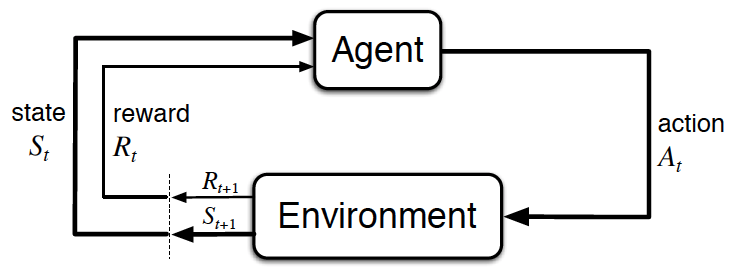
The agent-environment interaction in rl (Source: Sutton and Barto, 2017)
The agent-environment interaction in rl (Source: Sutton and Barto, 2017)

  • The reinforcement learning (RL) framework is characterized by an agent learning to interact with its environment.
  • At each time step, the agent receives the environment’s state (the environment presents a situation to the agent), and the agent must choose an appropriate action in response. One time step later, the agent receives a reward (the environment indicates whether the agent has responded appropriately to the state) and a new state.
  • All agents have the goal to maximize expected cumulative reward, or the expected sum of rewards attained over all time steps.

Episodic vs. Continuing Tasks

A task is an instance of the reinforcement learning (RL) problem.

  • Episodic task: tasks with a well-defined starting and ending point.
    • In this case, we refer to a complete sequence of interaction, from start to finish, as an episode
    • Episodic tasks come to an end whenever the agent reaches a terminal state
    • About past life regression and reincarnation 😳
    • Game
  • Continuing Tasks: interaction continues for ever, without limit 😬
    • Stocks

The Reward Hypothesis

All goals can be framed as the maximization of (expected) cumulative reward.

  • Problem of sparse rewards: when the reward signal is largely uninformative
  • Cumulative reward
    • The goal of the agent at time step T: maximize accumulative reward
    • The robot learns to move a bit slowly to sacrifice a little bit of reward but it will payoff because it will avoid falling for longer and collect higher accumulative reward
  • Discounted return: we give a discount rate $\gamma \in (0,1)$ to Reward at each step to avoid having to look too far into the limitless future
    • For larger values of $\gamma$, the agent cares more about the distant future.
    • Smaller values of $\gamma$ result in more extreme discounting
    • $\gamma = 0$: agent only cares about most immediate reward, not caring about the future
    • $\gamma = 1$: the return is not discounted. This becomes a pretty difficult task if the future is limitless
    • Most relevant for selection of actions in continuing tasks
    • Note: with or without the discount rate, the goal of agent is always the same

Markov Decision Process

A (finite) Markov Decision Process (MDP) is defined by:

    1. a (finite) set of Action $A$: space of all possible actions available to the agent
    1. a (finite) set of States $S$: all nonterminal states
    1. at a dicount rate $\gamma \in (0,1)$
    • $G_t = R_{t+1} + \gamma R_{t+2} + {\gamma}^2 R_{t+3} +…$
    • A common choice: $\gamma = 0.9$
    1. a (finite) set of Rewards $\gamma $
    1. the one-step dynamics of the environment: $p(s',\gamma |s,a) = \Bbb{P}(S_{t+1} = s', R_{t+1} =\gamma | S_t =s, A_t = a)$

The agent knows 1-3 and does not know 4 and 5. Therefore, the agent needs to learn from interaction to accomplish its goal.


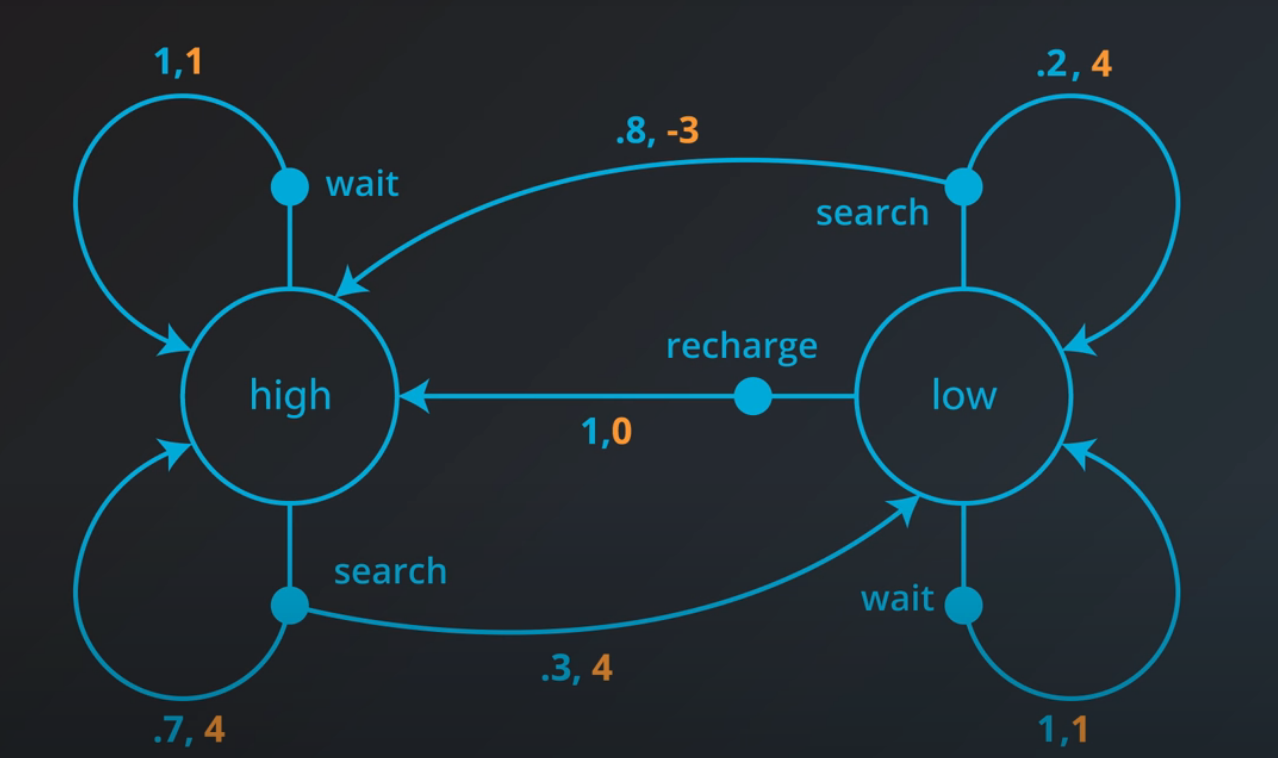
A MDP Problem

For a can-picking recycling robot:

  • He\gamma e is a method that the environment could use to decide the state and reward, at any time step.

    • $A$:
      • Search cans
      • Wait
      • Recharge
    • $S$:
      • High battery
      • Low battery

  • Say at an arbitrary time step t, the state of the robot’s battery is high ($S_t = \text{high}$). Then, in response, the agent decides to search ($A_t = \text{search}$). You learned in the previous concept that in this case, the environment responds to the agent by flipping a theoretical coin with 70% probability of landing heads.

    • If the coin lands heads, the environment decides that the next state is high ($S_{t+1} = \text{high}$), and the reward is $(R_{t+1} = 4$).
    • If the coin lands tails, the environment decides that the next state is low ($S_{t+1} = \text{low}$), and the reward is $(R_{t+1} = 4)$.
    • At an arbitrary time step $t$, the agent-environment interaction has evolved as a sequence of states, actions, and rewards. When the environment responds to the agent at time step $t+1$,
      • it considers only the state and action at the previous time step ($S_t, A_t$)
      • it does not consider any of ${ R_0, \ldots, R_t }$

  • For the case that $S_t = \text{high}$, and $A_t = \text{search}$, when the environment responds to the agent at the next time step, - with 70% probability, the next state is high and the reward is 4. In other words, $p(high,4|high,search) = \Bbb{P}(S_{t+1} = high, R_{t+1} = 4 | S_t = high, A_t = search) = 0.7$

  • Consider the following probabilities,

    • which of the above probabilities is equal to 0? (1,3,5)
    • Which of the above probabilities is equal to 1? (2,4)
      • (1) $p(\text{low}, 1|\text{low},\text{search})$
      • (2) $p(\text{high}, 0|\text{low},\text{recharge})$
      • (3) $p(\text{high}, 1|\text{low},\text{wait})$
      • (4) $p(\text{high}, 1|\text{high},\text{wait})$
      • (5) $p(\text{high}, 1|\text{high},\text{search})$

mdp-robot
Image from Udacity nd893


OpenAI Gym


Quiz

  • Consider an agent who would like to learn to escape a maze. Which reward signals will encourage the agent to escape the maze as quickly as possible?

Who is Markov?

Andrey Markov (1856–1922) was a Russian mathematician best known for his work on stochastic processes. A primary subject of his research later became known as Markov chains and Markov processes. Andrey Markov
Andrey Markov, image from Wikipedia