RL Solutions

Policies

• A deterministic policy: a mapping $\pi: S \to A$

  • For each state $s \in S$, it yields the action $a \in A$ that the agent will choose while in state $s$.
  • input: state
  • output: action
  • Example
    • $\pi(low) = recharge$
    • $\pi(high) = search$

• A stochastic policy: a mapping $\pi: S \times A \to [0,1]$

  • For each state $s \in S$ and action $a \in A$, it yields the probability $\pi(a|s)$ that the agent chooses action $a$ while in state $s$.

  • input: state and action

  • output: probability that the agent takes action $A$ while in state $S$

  • $\pi(a|s) =\Bbb{P}(A_t =a | S_t = s)$

  • Example

    • low
      • $\pi(recharge | low) = 0.5$
      • $\pi(wait | low) = 0.4$
      • $\pi(search | low) = 0.1$
    • high
      • $\pi(search | high) = 0.6$
      • $\pi(wait | high) = 0.4$

Gridworld Example

In this gridworld example, once the agent selects an action,

• it always moves in the chosen direction (contrasting general MDPs where the agent doesn’t always have complete control over what the next state will be),
• the reward can be predicted with complete certainty (contrasting general MDPs where the reward is a random draw from a probability distribution).
• the value of any state can be calculated as the sum of the immediate reward and the (discounted) value of the next state.

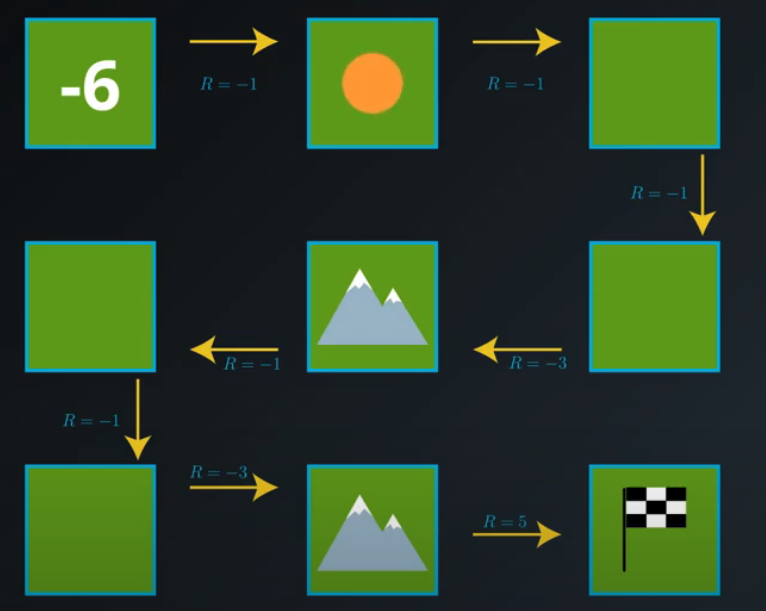
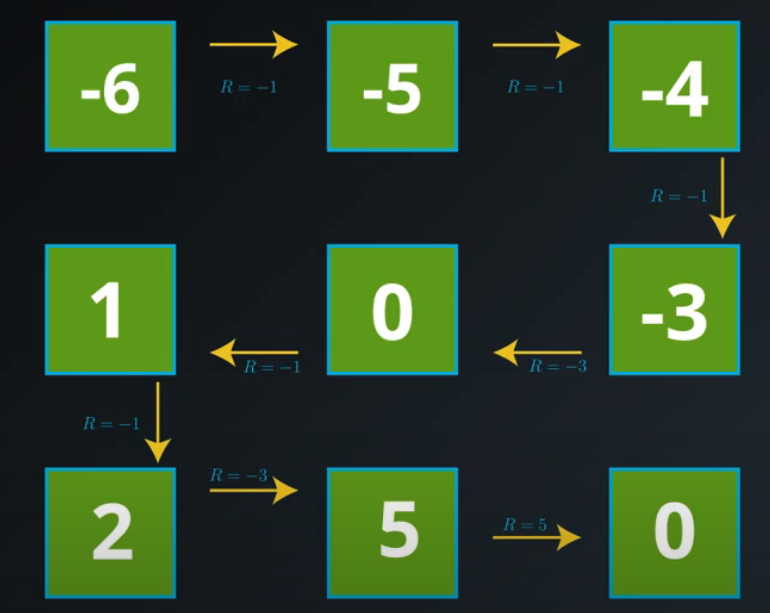
Grid Word images from Udacity nd893

State-Value Functions

The state-value function for a policy is denoted $v_\pi$. For each state $s \in {S}$, it yields the expected return if the agent starts in state $s$ and then uses the policy to choose its actions for all time steps.

• The value of state $s$ under policy $\pi$: $v_{\pi}(s) = \Bbb{E}_{\pi}[G_t|S_t = s]$

Bellman Equations

• Bellman equations attest to the fact that value functions satisfy recursive relationships.

• Read More at Chapter 3.5 and 3.6

• It expresses the value of any state $s$ in terms of the expected immediate reward and the expected value of the next state

  • $V_{\pi}(s) = \Bbb{E}_{\pi}[ R_{t+1} + {\gamma}v_{\pi}(S_{t+1}) | S_t) = s]$

• In the event that the agent’s policy $\pi$ is deterministic, the agent selects action $\pi(s)$ when in state $s$, and the Bellman Expectation Equation can be rewritten as the sum over two variables ($s'$ and $r$):

  • $v_{\pi}(s) = \sum_{s'\in{S^{+}}, r \in{R}} p(s', r|s, \pi{s})(r+ \gamma v_{\pi}(s'))$
  • In this case, we multiply the sum of the reward and discounted value of the next state $(r+ \gamma v_{\pi}(s'))$ by its corresponding probability $p(s', r|s, \pi{s})$ and sum over all possibilities to yield the expected value.

• If the agent’s policy $\pi$ is stochastic, the agent selects action $a$ with probability when in state $s$, and the Bellman Expectation Equation can be rewritten as the sum over three variables

  • $v_{\pi}(s) = \sum_{s'\in{S^{+}}, r \in{R}, a \in{A_{(s)}}} \pi(a|s) p(s', r|s, a) (\gamma + \gamma v_{\pi}(s'))$
    -In this case, we multiply the sum of the reward and discounted value of the next state $(\gamma + \gamma v_{\pi}(s'))$ by its corresponding probability $\pi(a|s) p(s', r|s, a)$ and sum over all possibilities to yield the expected value.

Action-value Functions

• The action-value function for a policy: $q_{\pi}$.
• The value $q_{\pi}(s,a)$ is the value of taking action $a$ in state $s$ under a policy $\pi$
• For each state $s \in S$ and action $a \in A$, it yields the expected return if the agent starts in state $s$, takes action $a$, and then follows the policy for all future time steps.
• $q_{\pi}(s,a) = \Bbb{E}_{\pi}[G_t |S_t =s, A_t = a ]$

Optimality

• A policy $\pi$ is defined to be better than or equal to a policy $\pi$ if and only if $v_{\pi \prime} (s) \ge v_{\pi} (s)$ for all.
• An optimal policy $\pi_\ast$ satisfies $\pi_\ast \ge \pi$ is guaranteed to exist but may not be unique.
• How do you define better policy?
  • Positive reward, which gives agent more motivation

Optimal State-value Function

All optimal policies have the same state-value function $v_\ast$

Optimal Action-value Function

All optimal policies have the same action-value function $q_\ast$

Optimal Policies

• Interaction ${\to}$ $q_\ast$ $\to$ $\pi_\ast$
• Once the agent determines the optimal action-value function $q_\ast$, it can quickly obtain an optimal polity $\pi_ast$ by setting
• $\pi(s) = argmax_{a \in A_{(s)}} q_\ast (s,a)$: Select the maximal actiona value $q$ at each step

Quiz

Calculate State-value Function $v_{\pi}$

• Assuming $\gamma = 1$, calculate $v_{\pi}(s_4)$ and $v_{\pi}(s_1)$

• Solve the problem using Bellman Equations
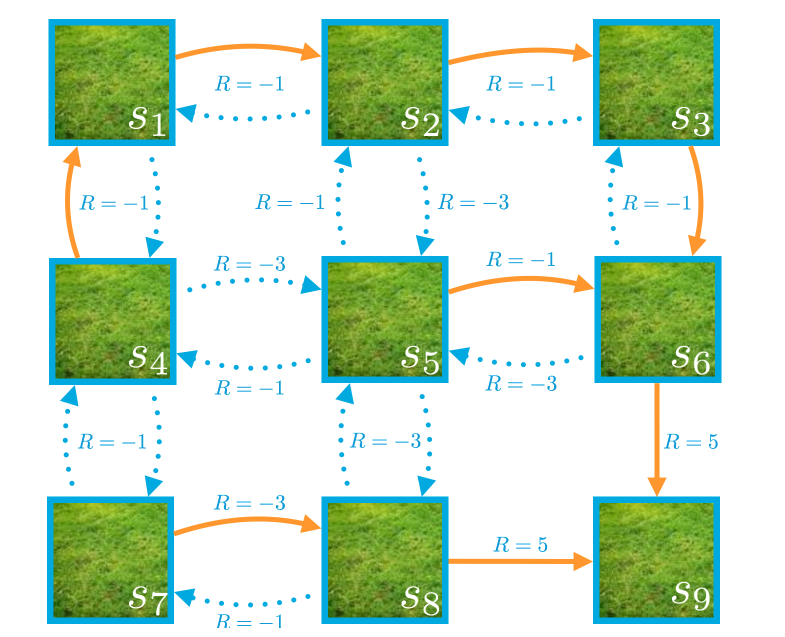
  Image from Udacity nd893

• Answer: $v_{\pi}(s_4) = 1$ and $v_{\pi}(s_1) = 2$

About Deterministic Policy

True or False?:
For a deterministic policy $\pi$:
$v_{\pi}(s) = q_{\pi}(s,\pi(s))$ holds for all $s \in S$.

Answer: True.

• It also follows from how we have defined the action-value function.
• The value of the state-action pair $s$, $\pi(s)$ is the expected return if the agent starts in state $s$, takes action $\pi(s)$, and henceforth follows the policy $\pi$.
• In other words, it is the expected return if the agent starts in state $s$, and then follows the policy $\pi$, which is exactly equal to the value of state $s$.

Optimal Policies

Consider a MDP (in the below table), with a corresponding optimal action-value function. Which of the following describes a potential optimal policy that corresponds to the optimal action-value function?

	a1	a2	a3
s1	1	3	4
s2	2	2	1
s3	3	1	1

Answer

• 1. State $s1$: the agent will always selects action $a3$
• 2. State $s2$: the agent is free to select either $a1$ or $a2$
• 3. State $s3$: the agent must select $a1$

• ← Previous
Next →