Introduction
Policy-Based Methods
- With value-based methods, the agent uses its experience with the environment to maintain an estimate of the optimal action-value function. The optimal policy is then obtained from the optimal action-value function estimate.
- Policy-based methods directly learn the optimal policy, without having to maintain a separate value function estimate.
Why
There are three reasons why we consider policy-based methods:
- Simplicity
- Policy-based methods directly get to the problem at hand (estimating the optimal policy), without having to store a bunch of additional data (i.e., the action values) that may not be useful.
- Stochastic policies
- Unlike value-based methods, policy-based methods can learn true stochastic policies.
- Continuous action spaces
- Policy-based methods are well-suited for continuous action spaces.
Policy Function Approximation
A stochastic policy
- The agent passes the current environment state as input to the network, which returns action probabilities.
- Then, the agent samples from those probabilities to select an action.
A Deterministic Policy
- The agent passes the current environment state as input to the network, which returns action probabilities.
- Then, the agent selects the greedy action
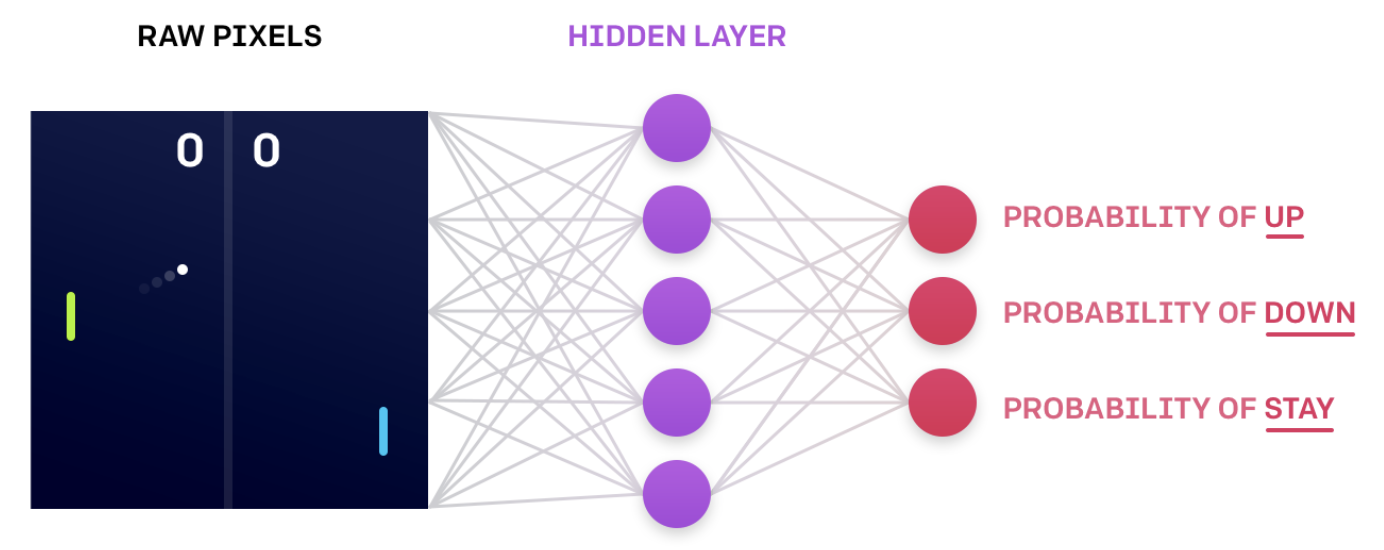
NN that encodes action probabilities (Source)
Discrete vs Continuous
- Discrete action spaces
- Cart Pole
- output layer: the probabilities for each action: 3 nodes
- output activation function: softmax
- Cart Pole
- Continuous action spaces
- Bipedal Walker
- output layer: 4 nodes
- output activation function: tanh
- Bontinuous Mountain Car
- output layer: 1 node
- output activation function: tanh
- Bipedal Walker
Gradient Ascent
- Gradient descent steps in the direction opposite the gradient, since it wants to minimize a function.
- $\theta \leftarrow \theta - \alpha \nabla_\theta U(\theta) $
- $\alpha$: step size
- Gradient ascent is otherwise identical, except we step in the direction of the gradient, to reach the maximum.
- $\theta \leftarrow \theta + \alpha \nabla_\theta U(\theta) $
- $\alpha$: step size
Local Minima
- A minimum within some neighborhood
- It may not be a global minimum.
Hill Climbing
- A mathematical optimization technique which belongs to the family of local search.
- An iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by making an incremental change to the solution.
- If the change produces a better solution, another incremental change is made to the new solution, and so on until no further improvements can be found.
Mathematical Definition
- Hill climbing is an iterative algorithm that can be used to find the weights $\theta$ for an optimal policy.
- At each iteration,
- we slightly perturb the values of the current best estimate for the weights $\theta_{best}$, to yield a new set of weights.
- These new weights are then used to collect an episode.
- If the new weights $\theta_{new}$ resulted in higher return than the old weights, then we set $\theta_{best} \leftarrow \theta_{new}$ .
Beyond Hill Climbing
- Steepest ascent hill climbing
- a variation of hill climbing that chooses a small number of neighboring policies at each iteration and chooses the best among them.
- Simulated annealing
- uses a pre-defined schedule to control how the policy space is explored, and gradually reduces the search radius as we get closer to the optimal solution.
- Adaptive noise scaling
- decreases the search radius with each iteration when a new best policy is found, and otherwise increases the search radius.
More Black-Box Optimization
- The cross-entropy method
- iteratively suggests a small number of neighboring policies,
- and uses a small percentage of the best performing policies to calculate a new estimate.
- The evolution strategies technique considers the return corresponding to each candidate policy.
- The policy estimate at the next iteration is a weighted sum of all of the candidate policies, where policies that got higher return are given higher weight.
Ref
- Evolution Strategies as a Scalable Alternative to Reinforcement Learning - OpenAI
- Open AI classic control environments
- An overview of gradient descent optimization algorithms
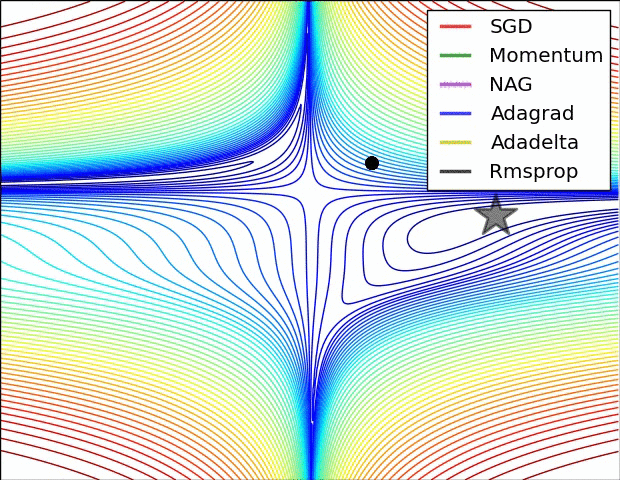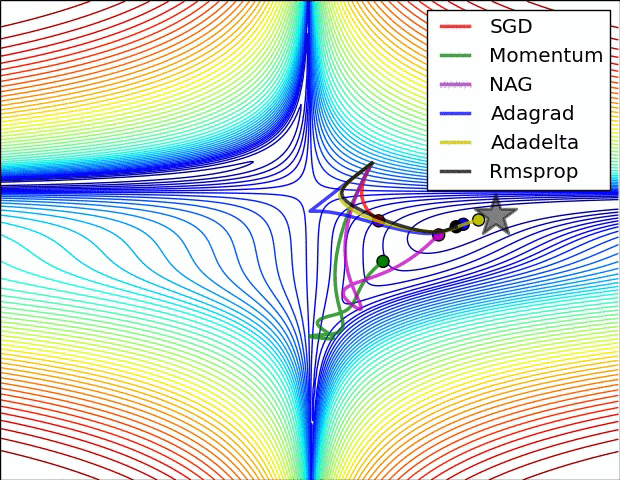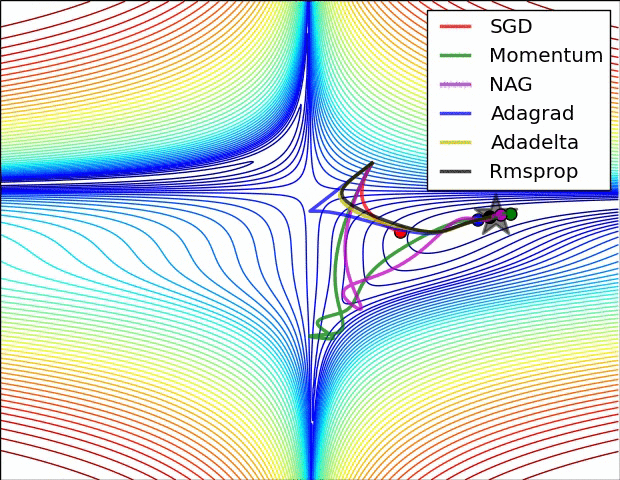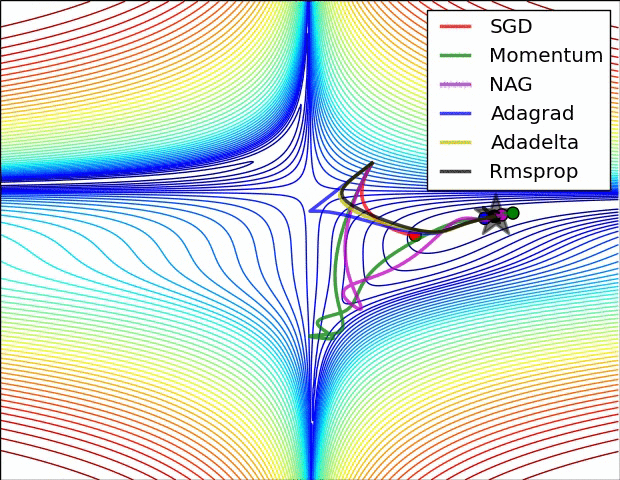
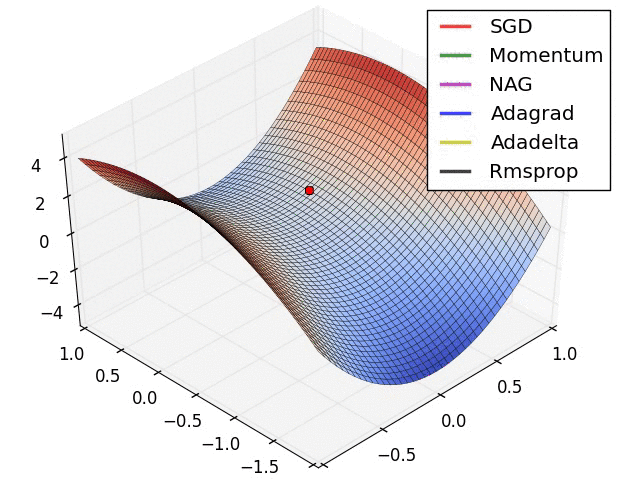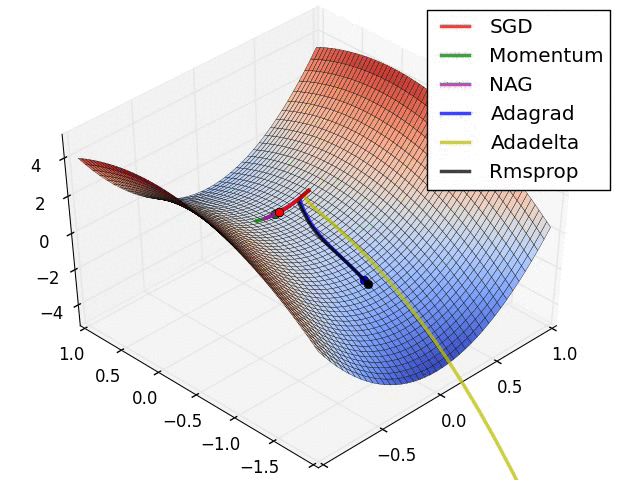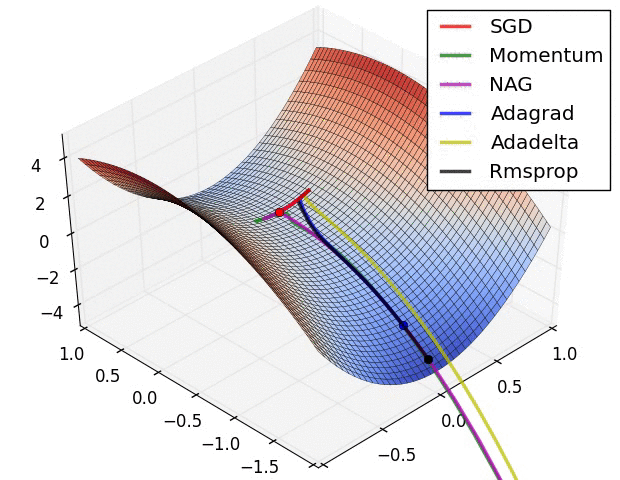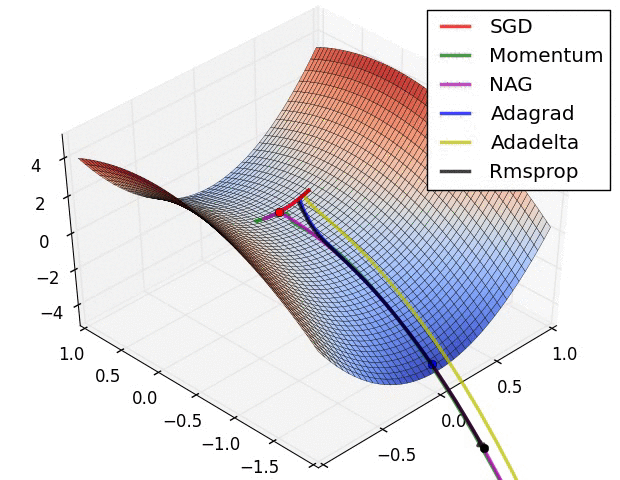
SGD optimization on loss surface contours