Policy Gradient


Policy Gradient Methods

RL vs. Supervised Methods

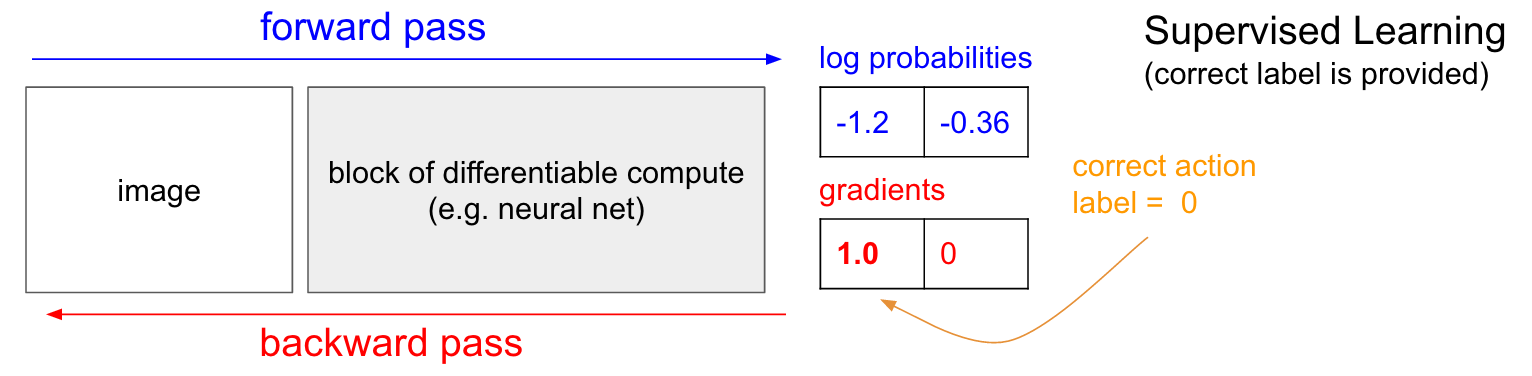
Supervised Learning
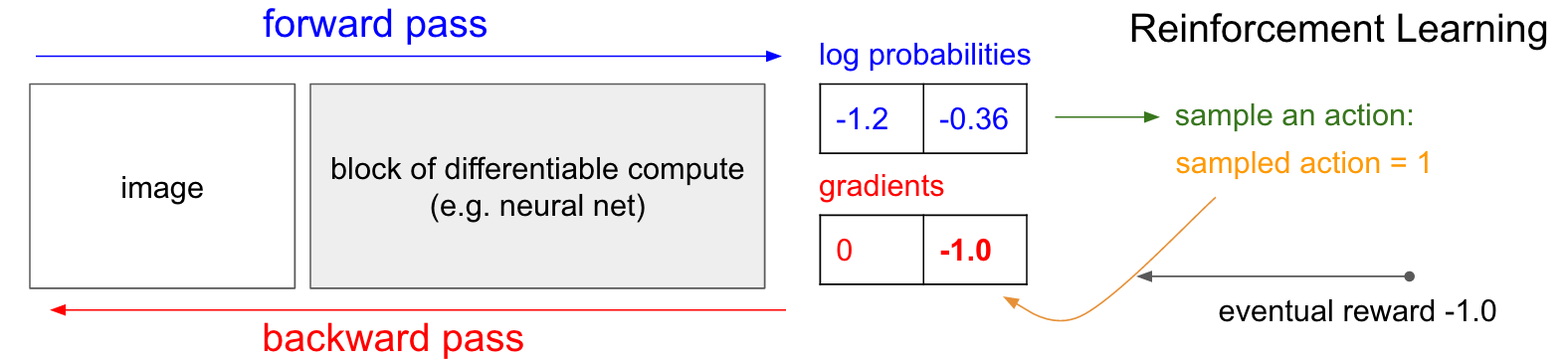
Reinforcement Learning
Connections between supervised learning and reinforcement learning (Source)


The Big Picture

The policy gradient method will iteratively amend the policy network weights to:

  • make (state, action) pairs that resulted in positive return more likely, 👍
  • make (state, action) pairs that resulted in negative return less likely. ⬇️

Reinforce

Reinforce
REINFORCE increases the probability of “good” actions and decreases the probability of “bad” actions. (Source)

Algorithm

  • Our goal is to find the values of the weights $\theta$ in the neural network that maximize the expected return $U$.

    • $U(\theta) = \sum_\tau P(\tau; \theta)R(\tau)$, where $\tau$ is an arbitrary trajectory (a sequence of states and actions)
    • One way to determine the value of $\theta$ that maximizes this function is through gradient ascent.
    • Once we know how to calculate or estimate this gradient, we can repeatedly apply this update step, in the hopes that $\theta$ converges to the value that maximizes $U(\theta)$.

  • $\theta \leftarrow \theta + \alpha \color{#af8dc3} {\nabla_\theta U(\theta)} $

    • $\alpha$ is the step size that is generally allowed to decay over time.

  • Estimate the gradient for one trajectory

      1. Collect an episode and trajectory $\tau =$ a full episode
      1. Change the weights of the policy network
        • $ \color{#af8dc3} {\nabla_\theta U(\theta)} \color{black} \approx \color{#af8dc3} {\hat{g}} \color{black} := \color{#1b7837} {\sum_{t=0} ^H} \color{black}\nabla_\theta log\color{blue}{\pi_\theta} \color{black} {(}\color{#1b7837} {a_t|s_t}\color{black}) R(\color{#1b7837} {\tau} \color{black})$
          • $ \color{black}\nabla_\theta log\color{blue}{\pi_\theta} \color{black} {(}\color{#1b7837} {a_t|s_t}\color{black}{)} $: direction of steepest increase of the $log$ probability of selecting action $a_t$ from state $s_t$
        • $R(\color{#1b7837} {\tau} \color{black})$: cumulative reward
          • If $\color{green}{Won}$: $R = +1$,
            • by taking a small step into the gradient
            • we can increase the probability of each $\color{#1b7837} {(S, a)}$ combination 👍
          • If $\color{red}{Lost}$: $R=-1$:
            • by taking a small step from the gradient
            • we can decrease the probability of each $\color{#1b7837} {(S, a)}$ combination ⬇️

  • Using $\color{blue}{m}$ trajectories to estimate the gradient $ \color{#af8dc3} {\nabla_\theta U(\theta)}$

      1. Use the policy $\color{blue}{\pi_\theta}$ to collect $m$ trajectories ${\tau^{(1)}, \tau^{(2)}, … \tau^{(m)}}$ with horizon $H$ (the last time step)
        • therefore, the $i$-th trajectory is $ \color{#1b7837} {\tau^{(i)}} \color{black} = (\color{#1b7837} {{s_0}^{(i)}, {a_0}^{(i)}, …, {s_H}^{(i)}, {a_H}^{(i)}, {s_{H+1}}^{(i)} }) $
      1. Estimate the gradient
        • trajectory $\tau \le$ a full episode
        • $ \color{#af8dc3} {\nabla_\theta U(\theta)} \color{black} \approx \color{#af8dc3} {\hat{g}} \color{black} := \color{blue} {\frac{1}{m} \sum_{i=1} ^m} \color{#1b7837} {\sum_{t=0} ^H} \color{black}\nabla_\theta log\color{blue}{\pi_\theta} \color{black} {(}\color{#1b7837} {a_t^{(i)}|s_t^{(i)}}\color{black}) R(\color{#1b7837} {\tau^{(i)}} \color{black})$
      1. Update the weights of the policy:
        • $\theta \leftarrow \theta + \alpha \color{#af8dc3} {\hat{g}} $
      1. Loop over steps 1-3.

Continuous Action Spaces

  • For an environment with a continuous action space, the corresponding policy network could have an output layer that parametrizes a continuous probability distribution.

  • For instance, assume the output layer returns the mean \muμ and variance $\sigma^2$ of a normal distribution

  • Then in order to select an action, the agent needs only to pass the most recent state $s_t$ as input to the network, and then use the output mean $\mu$ and variance $\sigma^2$ to sample from the distribution $a_t\sim\mathcal{N}(\mu, \sigma^2)$

  • This should work in theory, but it’s unlikely to perform well in practice! To improve performance with continuous action spaces, we’ll have to make some small modifications to the REINFORCE algorithm

Probability density function corresponding to normal distribution (Source: Wikipedia)
Probability density function corresponding to normal distribution (Source: Wikipedia)


(Optional) Derivation


Read