PyTorch Tutorial

Friday, May 08, 2020

Install PyTorch

conda install pytorch torchvision -c pytorch

Tensor

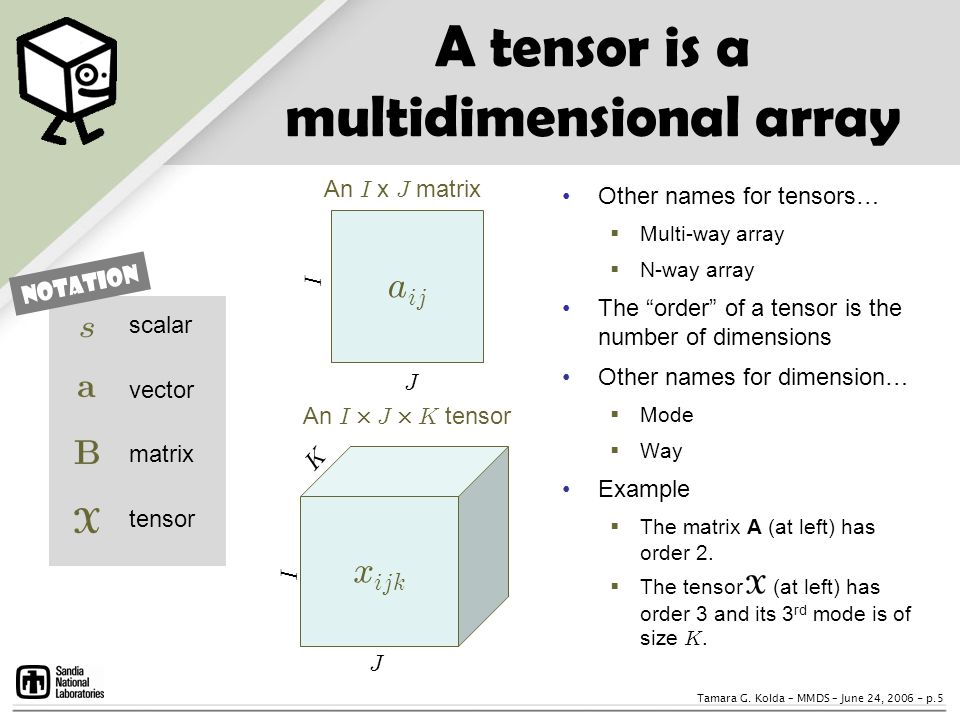
What is a Tensor?

Tensor: representated as N-dimensional array of data with certain transformation properties.
Tensor factorization: high-order generalization of matrix SVD or PCA
Matrix: a linear transformation

Tensor
Tensor

Methods of data reduction for a data tensor

How to initialize a Tensor?

From a list
From a numpy array
From another tensor. The shape and datatype are reained, unless explicitly overridden.

What are the attributes of a tensor?

Shape: a tuple (row, col) to dtermine the dimensionality of a tensor
dtype
device a tensor is running on
- cpu
- gpu

Tensor Operation API

Over 100 Operations
In-place operations: operations that have a _ suffix are in place
- tensor.add_(5)
- x.copy_(y)
Transposing
Indexing
Sliding
Mathmatical
- Multiply
  - use *
  - tensor.mul(tensor)
Linear Algebra
- Matrix Multiplication
  - tensor @ tensor.T
  - tensor.matmul(tensor.T)
Random Sampling
Tensor and Numpy
- Tensor to Numpy tensor.numpy()
- Numpy to Tensor torch.from_numpy()

Autograd

Notebook Tutorial

An automatic differentiation engine that powers NN training
Training a NN happens in two steps:
- Forward Propagation: In forward prop, the NN makes its best guess about the correct output. It runs the input data through each of its functions to make this guess.
- Backward Propagation: In backprop, the NN adjusts its parameters proportionate to the error in its guess. It does this by traversing backwards from the output, collecting the derivatives of the error with respect to the parameters of the functions (gradients), and optimizing the parameters using gradient descent. For a more detailed walkthrough of backprop

Computational Graph

Autograd keeps a record ot data(tensors) and all executed operations (along with resulting new tensors) in a directed acyclic graph (DAG) consisting of Function objects.

Tensors
- Leaves: input tensors
- Roots: output tensors
- From leaves to roots: run the requested operations
- From roots to leaves: compute the gradients using chain rules
Operations
- Forward pass
  - run the requested operation to compute a resulting tensor
  - maintain the operation’s gradient function in the DAG
- Backward pass
  - computes the gradients from each .grad_fn
  - accumulates them in the respective tensor’s .grad attributes
  - use the chain rule, propagates all the way to leaf tensors

DAGs

What are DAGs?
- DAGs are dynamic in PyTorch An important thing to note is that the graph is recreated from scratch; after each .backward() call, autograd starts populating a new graph.
- This is exactly what allows you to use control flow statements in your model; you can change the shape, size and operations at every iteration if needed.

Inclusion and Exclusion from the DAG

torch.autograd tracks operations on all tensors which have their requires_grad flag set to True.
For tensors that don’t require gradients, setting this attribute to False excludes it from the gradient computation DAG

x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)

a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
# False

b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
# True

Why exclusion is needed?

Frozen Parameters

Parameters that don’t compute gradients
Useful to freeze part of your model to offer some performance benefits by reducing autograd computations

Finetune a pretrained network

In finetuning, we freeze most of the model
Modify the classifier layers to make predictions on new labels

How to use exlusionary functionality?

Use a context manager in torch.no_grad()
Set requires_grad=False in a tensor

from torch import nn, optim

model = torchvision.models.resnet18(pretrained=True)

# Freeze all the parameters in the network!!!
for param in model.parameters():
    param.requires_grad = False

#  Finetune the model on a new dataset with 10 labels. 
# In resnet, the classifier is the last linear layer model.fc. 
# We can simply replace it with a new linear layer (unfrozen by default) that acts as our classifier
model.fc = nn.Linear(512, 10)

# Now all parameters in the model, except the parameters of model.fc, are frozen. The only parameters that compute gradients are the weights and bias of model.fc
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)

Neural Networks

How to construct a NN?

Use torch.nn package
Define the network
You just have to define the forward function
The backward function (where gradients are computed) is automatically defined for you using autograd.
You can use any of the Tensor operations in the forward function.
The learnable parameters of a model are returned by net.parameters()

convnet
convnet

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
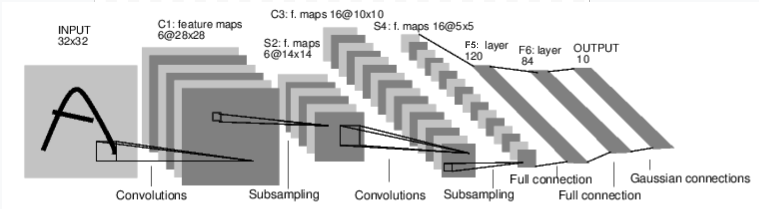
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension 
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

# params
params = list(net.parameters())
print(len(params))
print(params[0].size())

Reference

← Previous