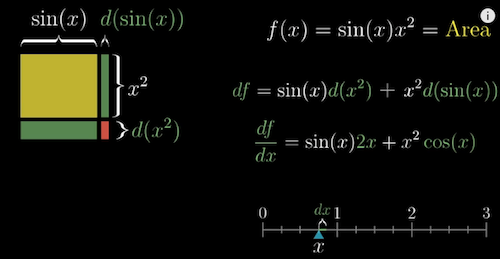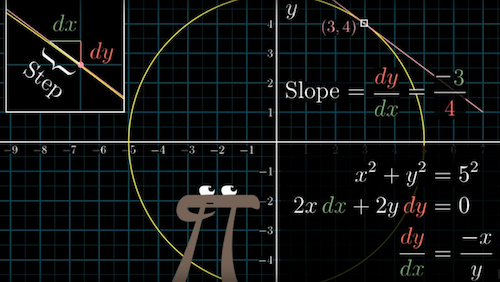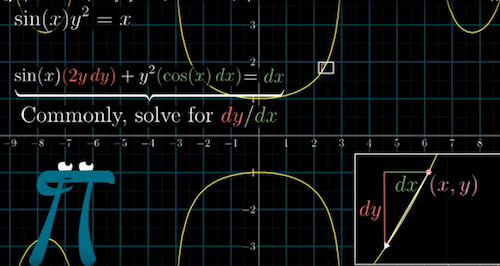Calculus
Table of Contents
- Calculus
- Derivatives and integrals
- The paradox of the derivative
- Chain rule and product rule
- Derivatives of exponentials
- Implicit differentiation
- Limits, L’Hopital’s rule, and epsilon delta definitions
- Integration and the fundamental theorem of calculus
- The average of a continuous variable
- Higher order derivatives
- Taylor series
- References
Calculus
- A philosophy about concrete finitely small nudge

- Fathers of calculus, 1:05
Derivatives and integrals
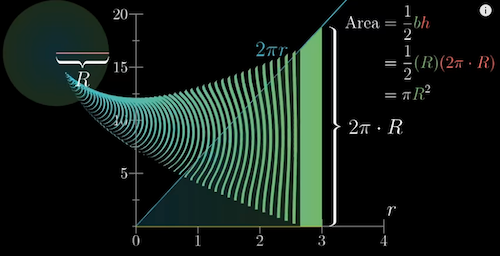
How to calculate the area of a circle?
-
The area of a circle can be approximated to the aggregated areas of many rectangles ($2\pi rdr$, perimeter $2\pi r$ as the length*width $dr$)
The paradox of the derivative
-
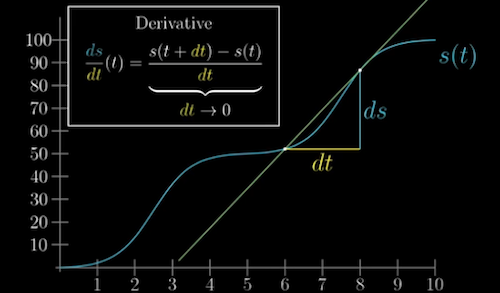
Derivative: to calculate the derivative at one time point (e.g. velocity), we actually need two time points (to calculate $\frac{Distance Change}{TimeChange}$)
-
Make the time point interval $\to$ 0
-
The derivative as an instaneous rate of change = The best constant approximation of the rate of change
-
The slope of the line tangent to the point at t $\to$
Chain rule and product rule
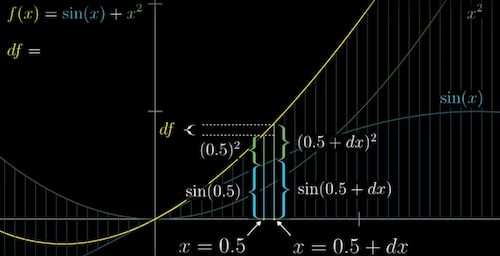
- Sum rule: The derivative of a sum is the sum of derivatives
-
$\frac{d}{dx}(g(x)+h(x)) = \frac{dg}{dx} + \frac{dh}{dx}$
-
e.g. $\frac{d}{dx}(sin(x)+x^2 = cos(x) + 2x$
- Product rule: try to use an area for visualization
-
Numerically: Left d(Right) + Right d(Left)
-
$f(x) = g(x)h(x)$
-
$df = g(x)dh + h(x)dg$
-
$\frac{df}{dx} = g(x)\frac{dh}{dx} + h(x)\frac{dg}{dx}$
- Function composition
-
Chain Rule: $\frac{d}{dx}g(h(x)) = \frac{dg}{dg}(h(x))\frac{dh}{dx}(x)$
-
A small change in x $\to$ A small change in the intermediate number $\to$ Nudge the change in the final value
Derivatives of exponentials
- The Euler’s number e
-
$e = 2.71828$
-
$M(t) = e^t$
-
Numerically: $\frac{dM}{dt}(t) =\frac{e^0.00000001 -1}{0.00000001} =e^t(1.000000000)$
-
Geometrically: The slope of a tangent line to any point on the $e^t$ graph equals the height of that point at the horizontal axis
- Use the chain rule for other exponential functions
- $2 = e^{(ln(2))}$
- $2^t = e^{(ln(2))t}$, the exponential function of 2
- $ln(2)2^t = ln(2)e^{ln(2)t}$, the derivative
Implicit differentiation
- Implicit curve: a plane curve defined by an implicit equation relating two coordinate variables, commonly x and y
- Example
-
$x^2 + y^2 =5$ the implicit curve function
-
$2xdx + 2ydy = 0$ the implicit differentiation process. $0$ means we want $x^2 + y^2$ not change
-
$\frac{dx}{dy} = \frac{-x}{y}$ the slope of the tangent line to the circle
-
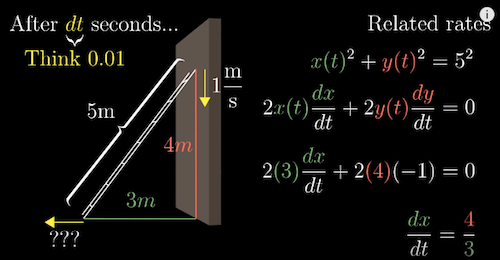
- A related rates problem: how the rates of change for each of the values depend on each other
- Example
-
$x(t)^2 + y(t)^2 =5$ pythagorean theorem, x and y are functions of time, the top of the ladder $y$ is dropping at $1m/s$, find out the rate of the bottom of the ladder that is moving from the wall at the initial moment
-
- Two more multivariable calculus problem: try to have a clear understanding of how what tiny nudges are playing and how they depend on each other
- Example 1
-
$sin(x)y^2 =x$, represent a bunch of points $(x,y)$ on the curves
-
$sin(x)(2ydy) + y^2cos(x)dx = dx$ Geometrically, this means the left and the right side change must be the same to keep the points on the curves
-
$\frac{dy}{dx} = \frac{1-y^2}{2tan(x)y}$
-
- Example 2
-
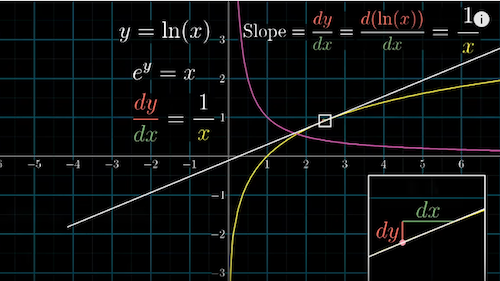
$y =ln(x)$, $\frac{dy}{dx} = \frac{d(ln(x))}{dx}$
-
$e^y =x$, $\frac{dy}{dx} = \frac{1}{x}$
-
$\frac{dy}{dx} = \frac{1}{x}$
-
Limits, L’Hopital’s rule, and epsilon delta definitions
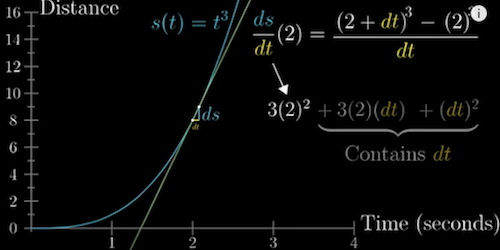
- The official definition of derivative
- The rise-over-run slope between the starting point on the graph and the nudged point when the difference between the input and nudged input is close to 0 ($dx$)
- $$\frac{df}{dx}(x)=\lim_{dx\to 0}\frac{f(x+dx)-f(x)}{dx}$$
- Replace dx with a commonly used variable h (or $\Delta x$ )
- $$\frac{df}{dx}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$
- The epsilon delta definition
-
The formalization of the notion of limit (one value approach to another)
-
Baron Augustin-Louis Cauchy first used, Bernard Bolzano gave the definition
-
The dependent expression f(x) approaches the value L as the variable x approaches the value c if f(x) can be made as close as desired to L by taking x sufficiently close to c.
-
- L’Hopital’s rule
- Johann Bernoulli $\to$ Guillaume de l’Hôpital
- When you are solving a limit, and get $0/0$ or $∞/∞$, L’Hôpital’s rule is the tool you need
- Conditions:
- $$\lim_{x\to c}f(x) =\lim_{x\to c}g(x) = 0$$
- $$\lim_{x\to c}f(x) =\lim_{x\to c}g(x) = \pm \infty$$
- Conclusion:
- $$\lim_{x\to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}$$
Integration and the fundamental theorem of calculus
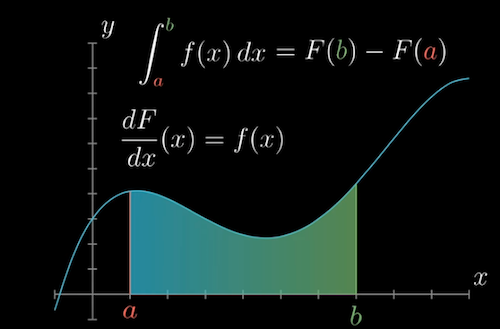
- Integral: the fundamental theorem of calculus
-
The sum of a large number of small values on the continuum between the lower bound a and upper bound b
-
Given a function $f(x)$, find $F(x)$, the antiderivative of $f(x)$
-
The reverse relation of derivative ($f(x)$ is the derivative of F ⟺ $f$ is an antiderivative of $f'$)
-
Calculate he integral of $f(x)$: $\int_a^b f(x)dx = F(b) - F(a)$
-
Each function has a family of antiderivatives (the difference between the family members is the constant $C$)
-
Geometrically: integrals don’t measure the area per se, they measure the signed area
-
The average of a continuous variable
- Cyclic phenomenon are modelled using sin waves
- Example
- Average height $= \frac{Area}{Width} = \frac{\int_0^\pi \sin(x)dx}{\pi}$
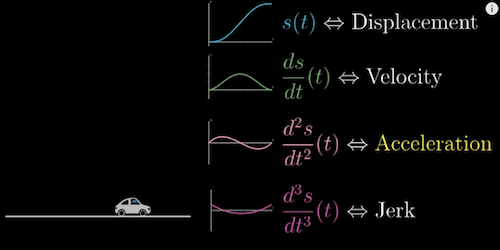
Higher order derivatives
Taylor series
-
Scottish mathematician James Gregory and formally introduced by the English mathematician Brook Taylor
-
Used for approximate functions: to find the polynomial functions for non-polynomial functions
-
A general nth-degree polynomial $f(x) = a_0 + a_1(x-c)+ a_2(x-c)^2 +a_3(x-c)^3+…$
- Closed form: $f(x) = \sum_{j=0}^{\infty} a_j(x-c)^j$
-
$f(x) = \frac{f(c)}{0!} +\frac{f’(c)}{1!}(x-c) +\frac{f’’(c)}{2!}(x-c)^2 + \frac{f’’’(c)}{3!}(x-c)^3+…$
- Closed form: $f(x) = \sum_{j=0}^{\infty} \frac{f^{(j)}(c)}{j!}(x-c)^j$
-
Maclaurin’s series: when c=0