Linear Algebra

how to execute algorithms on massive datasets

Table of Contents

Vector

  • Imagine we have a two dimensional space composed of x and y axis, and their intersection called origin (0).
  • $\begin{bmatrix}1 \\2 \end{bmatrix}$ : The coordinate of a vector is a pair of numbers which gives instructions to tell the vector how to get from the origin of the vector to the tip of the vector.
  • The first number tells you how far to walk on the x-axis
  • After that, the second number tells you how far to walk parallel to the y-axis
  • To differentiate vectors from points, the convention is to write these two numbers vertically in a square bracket.
  • Every pair of numbers is associated with one and only one vector, vice versa
  • Vectors, what even are they? 3'- 4'

Determinant

2-D

  • $A = \begin{bmatrix}a&b \\c&d \end{bmatrix}$
  • Determinant of $A$: $det(A)$
  • Numerically
    • a scalar value that can be computed from the elements of a square matrix and measures the scaling of linear transformation described by the matrix
    • $det(A)= ad-bc$
  • Geometrically
    • $det(A)$:the area scaling factor of the linear transformation
    • $\lvert det(A) \rvert > 1$, increase the area by a factor of 5
    • 0< $\lvert det(A) \rvert < 1$: squish down area
    • Zero determinant: when $det(A) =0$, the transformation squishes down the area to a line or a point
    • $det(A) < 0$: the orientation of space is inverted (space is inverted. The basis vector $\vec{i}$ is now on the left side of $\vec{j}$)

3-D

  • $B = \begin{bmatrix}u_1&v_1&w_1 \\u_2&v_2&w_2 \\u_3&v_3&w_3 \end{bmatrix}$
  • Numerically:
    • $det(B)$: the volume scaling factor of the linear transformation described by the matrix
    • $det(B) = u_1(v2w3-w2v3)-v_1(u_2w_3-w_2u_3)+w_1(u_2v_3-v_2u_3)$
  • Geometrically
    • $det(B) < 0$: Right finger rule no longer fits
      • index finger: points to the direction of $\vec{i}$
      • middle finger: points to the direction of $\vec{j}$
      • thumb: points to the direction of $\vec{k}$

Dot products

  • Two vectors of the same dimension

    • $\vec{v}$ = $\begin{bmatrix}1 \\2 \end{bmatrix}$

    • $\vec{w}$ = $\begin{bmatrix}3 \\4 \end{bmatrix}$

  • Order: doesn’t matter

  • Numerically

    • Pair the coordinates of multiply them together and add the result
    • $\begin{bmatrix}1 \\2 \end{bmatrix}$ $\cdot$ $\begin{bmatrix}3 \\4 \end{bmatrix}$ = 1 $\cdot$ 3+ 2 $\cdot$ 4 = 11

  • Geometrically

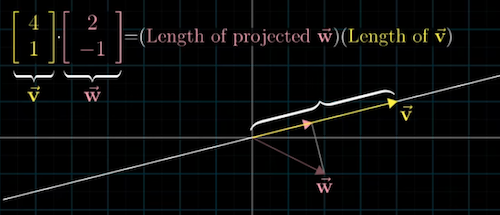
    • Project $\vec{w}$ onto the line passing through the origin on the tip of $\vec{v}$
    • $\vec{v}$ $\cdot$ $\vec{w}$ = (length of projected $\vec{w}$) $\cdot$ (length of projected $\vec{v}$)
    • Dot product vs Directions
      • $\vec{v}$ $\cdot$ $\vec{w}$> 0: vectors are pointing to similar directions
      • $\vec{v}$ $\cdot$ $\vec{w}$< 0: vectors are pointing to opposing direction
      • $\vec{v}$ $\cdot$ $\vec{w}$ = 0: vectors are perpendicular

  • Duality: natural-but-surprising correspondence

    • Matrix vector product:
      [$u_x$ $u_y$] $\begin{bmatrix}x \\y \end{bmatrix}$ = $u_x$ $\cdot$ $x$ + $u_y$ $\cdot$ $y$
    • Dot product:
      $\begin{bmatrix}u_x \\u_y \end{bmatrix}$ $\cdot$ $\begin{bmatrix}x \\y \end{bmatrix}$ = $u_x$ $\cdot$ $x$ + $u_y$ $\cdot$ $y$

dot product projection

Screenshot at 2:19 in video

Cross products

  • The standard basis vectors $\vec{i}$, $\vec{j}$, and $\vec{k}$

  • Two vectors of the same dimension

    • $\vec{v}$ = $\begin{bmatrix}v_1 \\v_2\\v_3 \end{bmatrix}$

    • $\vec{w}$ = $\begin{bmatrix}w_1 \\w_2 \\w_3\end{bmatrix}$

  • Order: matters

  • Cross products

    • $\vec{p}$ = $\vec{v}$ $\times$ $\vec{w}$
    • $\vec{p}$ is a vector that is perpendicular to both $\vec{v}$ and $\vec{w}$ and thus normal to the plane containing them

  • $\vec{p}$ directions

    • $\vec{p}$ > 0: when $\vec{v}$ is on the right side of $\vec{w}$
    • $\vec{p}$ < 0: when $\vec{v}$ is on the left side of $\vec{w}$

  • Numerically

    • $\begin{bmatrix}v_1 \\v_2\\v_3 \end{bmatrix}$ $\times$ $\begin{bmatrix}w_1 \\w_2 \\w_3\end{bmatrix}$ = ($v_2w_3 -w_2v_3)\vec{i}$ + ($v_3w_1$ - $v_1w_3)\vec{j}$ + ($v_1w_2$ - $v_3w_1)\vec{k}$

  • Geometrically

    • The positive area of the parallelogram having $\vec{v}$ and $\vec{w}$ as sides
    • The length of $\vec{p}$ = the area of parallelogram defined by $\vec{v}$ and $\vec{w}$
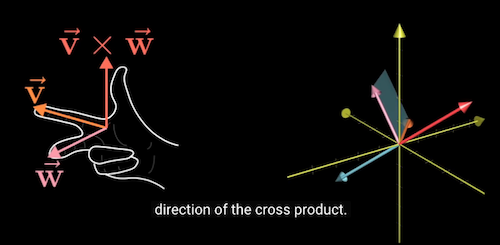
    • The direction of $\vec{p}$ is defined using the Right Hand Rule
      • index finger: points to the direction of $\vec{v}$
      • middle finger: points to the direction of $\vec{w}$
      • thumb: points to the direction of $\vec{p}$

cross product projection

Screenshot at 6:03 in video


Cramer’s rule

  • Cramer’s rule expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-hand-sides of the equations. It is named after Gabriel Cramer
  • Consider a system of linear equation

  • $ax + by =e$
    $cx+dy=f$

  • $\frac{e-ax}{b}=\frac{f-cx}{a}$; $x = \frac{ed-bf}{ad-bc}$

  • $\frac {e-by} {a} = \frac{f-dy}{c}$; $y = \frac{af-ec} {ad=bc}$

  • Matrix Equation

  • $\begin{bmatrix}a&b \\c&d \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix} = \begin{bmatrix}e \\f \end{bmatrix}$

  • $x = \frac { \begin{array}{| cc |} e&b\\ f&d\end{array} } { {\begin{array}{|cc|} a&b\\c&d\end{array} } }$

  • $y = \frac { \begin{array}{|cc|} a&e\\c&f\end{array} } { {\begin{array}{|cc|} a&b\\c&d\end{array} } }$


Linear transformations

What is linear transformation?

  • A function that takes an input vector and generates an output vector
  • The word ‘transformation’ suggests that we think using movement
  • The word ‘Linear’ suggests all spatial grid lines (for visualizing the coordinate system) must remain parallel and evenly spaced (not curvy), and the origin remains fixed (not moving).

What is a shear matrix?
A shear matrix is an elementary matrix that represents the addition of a multiple of one row or column to another.

  • $\begin{bmatrix}1&s \\0&1 \end{bmatrix}$
  • $\begin{bmatrix}1&0 \\s&1 \end{bmatrix}$

How is matrix useful?

  • Computer graphics
  • Robotics: e.g. rotation
  • Solve system equations: Linear system

Matrix vector multiplication

  • Numerically:
    • $\begin{bmatrix}a&b \\c&d \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix} = x\begin{bmatrix}a \\c \end{bmatrix} + y\begin{bmatrix}b \\d \end{bmatrix} = \begin{bmatrix}{ax+by} \\ {cx+dy} \end{bmatrix}$
  • Geometrically: apply a transformation to a vector
    • Think of the columns of a matrix as transformed basis vectors $\begin{bmatrix}a \\c \end{bmatrix}$ and $\begin{bmatrix}b \\d \end{bmatrix}$
    • The linear trans result is the linear combination of the transformed basis vectors

Matrix multiplication

  • Numerically: Right to left
    • $\begin{bmatrix}a&b \\c&d \end{bmatrix}\begin{bmatrix}e&f \\g&h \end{bmatrix} =\begin{bmatrix}{ae+bg}&{af+bh} \\ {ce+dg}&{cf+dh}\end{bmatrix}$
    • Step1: $\begin{bmatrix}a&b \\c&d \end{bmatrix}\begin{bmatrix}e \\g \end{bmatrix} = e\begin{bmatrix}a \\c \end{bmatrix} + g\begin{bmatrix}b \\d \end{bmatrix} = \begin{bmatrix}{ae+bg} \\ {ce+dg} \end{bmatrix}$
    • Step 2: $\begin{bmatrix}a&b \\c&d \end{bmatrix}\begin{bmatrix}f \\h \end{bmatrix} = f\begin{bmatrix}a \\c \end{bmatrix} + h\begin{bmatrix}b \\d \end{bmatrix} = \begin{bmatrix}{af+bh} \\ {cf+dh} \end{bmatrix}$
  • Geometrically:
    • $f(g(x))$
    • Composition: apply one transformation $f$ after another $g$
  • Order: matters $M_1M_2 \ne M_2M_1$
  • Associativity: $(AB)C=A(BC)$, meaning applying transformation C, B, and A

Change of basis

  • Translate between two coordinate systems
  • An inverse transformation $A^{-1}$ means: reverse the transformation
  • $A^{-1}MA$
    • $M$: a transformation in coordinate system P
    • $A^{-1}$ and $A$: mathematical sort of empathy
    • $A^{-1}MA$: mathematical product in coordinate system Q

Eigenvectors and eigenvalues

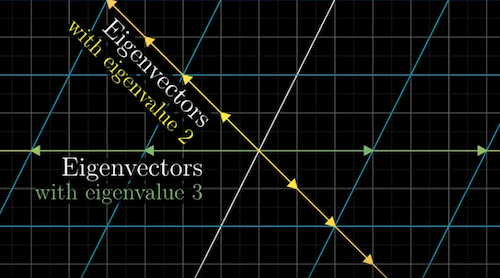
  • Eigenvector: a vector that stays on its own span (the line passing through the origin and the tip of the vector) during a matrix transformation, unlike other vectors that are knocked off their spans during transformation

  • Eigenvalue: The factor by which the eigengectors is stretched or squished

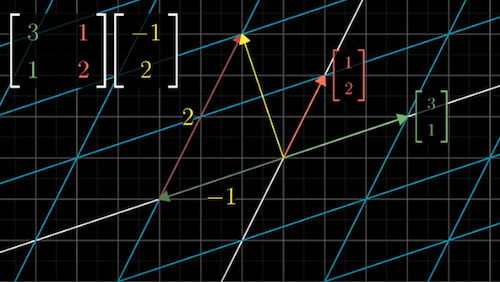
  • e.g. Matrix $A = \begin{bmatrix}3&1 \\0&2 \end{bmatrix}$ Eigenvector $\vec{v}$ = $\begin{bmatrix}-1 \\1 \end{bmatrix}$, eigenvalue of $\vec{v}$ is 2

  • eigen
    Eigenvector 3:39

  • The axis of a 3-D rotation: the span of an eigenvector, with eigenvalue equal to 1 (no stretching or squishing during rotation)

  • Eigenbasis: a set of basis vectors which are also eigenvectors

    • useful for matrix operations,
    • e.g. To calculate $\begin{bmatrix}3&1 \\0&2 \end{bmatrix}^{100}$, change the basis vector to eigenbasis system $\begin{bmatrix}1&-1 \\0&1 \end{bmatrix}$
    • $\begin{bmatrix}1&-1 \\0&1 \end{bmatrix}^{-1}$ $\begin{bmatrix}3&1 \\0&2 \end{bmatrix}$ $\begin{bmatrix}1&-1 \\0&1 \end{bmatrix}$ = $\begin{bmatrix}3&0 \\0&2 \end{bmatrix}$

  • How to calculate the eigenvalue of a matrix?

    • Matrix-vector multiplication $A\vec{v} = \lambda\vec{v}$ Scalar multiplication
    • Change the scalar multiplication to matrix multiplication ($I\vec{v}$) scaled by a factor $\lambda$
    • $A\vec{v} = \lambda I \vec{v}$; matrix-vector multiplication on both sides
    • $I = \begin{bmatrix}1 &0 \\0&1 \end{bmatrix}$, the identity matrix with ones in the diagonal
    • $(A-\lambda I)\vec{v} = 0$
    • For non-zero $\vec{v}$, the transformation associated with the matrix has to be squished down to a lower dimension (squishification), which corresponds to a zero determinant of the matrix $det(A-\lambda I) = 0$
    • e.g.

      • For matrix $A = \begin{bmatrix}3&1 \\0&2 \end{bmatrix}$

      • $\biggl(\begin{bmatrix}3&1 \\0&2 \end{bmatrix} - \lambda\begin{bmatrix}1 &0 \\0&1 \end{bmatrix}\biggr)\vec{v}=0$

      • $det \biggl(\begin{bmatrix}{3-\lambda}&1 \\0&{2-\lambda } \end{bmatrix}\biggr) = 0$

      • $(3-\lambda)(2-\lambda)=0$

      • $\lambda$ can only be an eigenvalue, therefore, $\lambda=2$ or $\lambda=3$, which are the eigenvectors of matrix $A$


Abstract vector spaces

  • Function: a type of vectors

Questions

  • What does a determinant of 0 mean for a matrix transformation?

    • $det(A)=0$
    • The matrix is squished down to a lower dimension

  • What kind of matrices have no eigenvalues?

    • Non-square matrix
    • A skew-symmetric matrix (or anti-symmetric matrix) where $A^T=-A$

  • What properties do linear transformations have?

    • Linear transformations preserve addition and scalar multiplication
    • Preserving additivity: The result of adding two vectors and applying transformation to the sum is the same as adding the transformed vectors.
      $L(\vec{v}+\vec{w})=L(\vec{v})+L(\vec{w})$
    • Preserving scaling: when you scale a vector by a scaler and then apply the transformation is the same as scaling the transformed vector.
    • These properties make it possible to represent any vector and do matrix multiplications. $L(c\vec{v})=cL(\vec{v})$

Glossary

  • Column space: all the linear combinations of the column vectors Video by Sal Khan
  • Identity transformation: the transformation that does nothing
  • Gaussian elimination
  • Inverse matrices: the inverse transformation in geometry (clockwise-counterclockwise, rightward shear – leftward shear) $A^{-1}*A^1=\begin{bmatrix}0&1 \\1&0 \end{bmatrix}$
  • Rank: the number of dimensions in the output of a transformation (e.g. Rank 2: All vectors after a transformation land on a 2-D plane)
  • Null space (kernel): the space of all vectors becoming null
  • Row echelon form
  • Span: the set of all linear combinations of two vectors.
  • Symmetric matrix: $A^T=A$
  • Skew-symmetric matrix $A^T=-A$

Read More