Birthday
What is pigeonhole principle?
If $n$ items are put into $m$ containers, with $n > m$ then at least one container must contain more than one item.
What is the probability of two people among $k$ people having the same birthday?
- If $k > 366$, $P = 1$
- If $k<366$, what is the minimal $k$ to get $P \approx 0.5$?
- $P_{no match} = \frac{365 \cdot 364 \dots (365-k+1)}{365^k}$
- $P_{match} = 1- P_{no match}$
- $0.51$, $k =23$
- $0.97$, $k =50$
- $0.99999$, $k =100$
- Let’s build some intuition of $P_{match} = \binom{k}{2}$
- $\binom{23}{2} = \frac{23 \cdot 22}{2} =253$
Probability Properties
- $P_{(A^c)} = 1-P_{(A)}$
- $P_{(A)} \le P_{(B)}$ if $A$ is contained in $B$ ($A \in B$)
- $B= A {\bigcup} (B \bigcap A^c)$, disjoint
- $P_{(B)} = P_{(A)} + P_{(B \bigcap A^c)} \ge P_{(A)}$
- $P_{A \bigcup B} =P_{(A)} + P_{(B)} - P_{(A \bigcap B)}$
- $P_{A \bigcup B \bigcup} =P_{(A)} + P_{(B)} + P_{(C)} - P_{(A \bigcap B)}- P_{(A \bigcap C)}- P_{(B \bigcap C)} + P_{(A \bigcap B \bigcap C)}$
- General Case
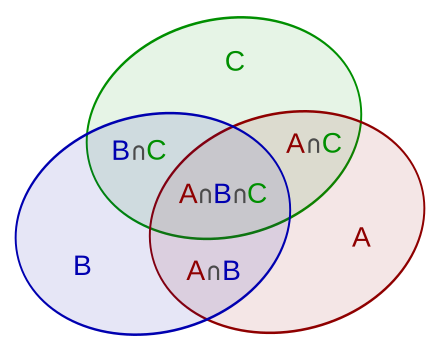
Inclusion–exclusion illustrated by a Venn diagram for three sets
De Montmort’s Problem
- 1713
- matching problem for gambling
- $n$ cards, labeled $1, 2, 3, …, n$, let $A_j$ be the event with matches
- $P_{(A_1 \bigcup A_2 \bigcup \dots \bigcup A_n)} \approx 1- \frac{1}{e}$

